Experimental Mathematics

Colorful fractional Gaussian integers

Fractional Gaussian integers are complex numbers that, when mapped onto the complex plane, reveal fascinating geometric patterns and symmetries.

• 2025, Colorful fractional Gaussian integers (EML, University of Luxembourg, in collaboration with Anne Fisch)

Mathematical puzzles

Mathematical puzzles and games explored through algorithms and strategy, including the mathematics behind Wordle, strategies for Mastermind, and creative variations on Sudoku.

• 2024, "Die Mathematik hinter Wordle-Raten" (Mathe am Computer, Universität Paderborn)
• 2024, "Wie besiege ich Mastermind?" (Mathe am Computer, Universität Paderborn)
• 2024, "Sudoku mal anders!" (Mathe am Computer, Universität Paderborn)

Visualising systems of linear equations

One can visualise sets of integral solutions of systems of linear equations (e.g. those representing magic squares or similar objects) with integral coefficients, and their reduction modulo an integer. For example, by colouring the solutions, where an entry in a solution (vector) which is 0 mod 2 could be represented by black square and 1 mod 2 by a white one. The aim of this project was to better understand systems of linear equations, whilst trying to produce beautiful images using rainbow spectrum, or also RGB (red-green-blue), CMY (cyan- magenta-yellow) systems, or Opacity, etc.

• 2024, Visualising systems of linear equations (EML, University of Luxembourg, in collaboration with Gabor Wiese)
• 2024, "Einfärbung eines magischen linearen Gleichungssystems" (Mathe am Computer, Universität Paderborn)

• Animation 1
• Animation 2

Celebrating the 20th anniversary of our university
with Fourier series

One can create many two-dimensional "one-line drawings" with complex Fourier series. The aim of this project was to do this for some interesting logos, such as the Unilu university and the 'Roude Léiw' logo.

• 2023, Celebrating the 20th anniversary of our university with Fourier series (EML, University of Luxembourg)

• Roude Léiw drawing

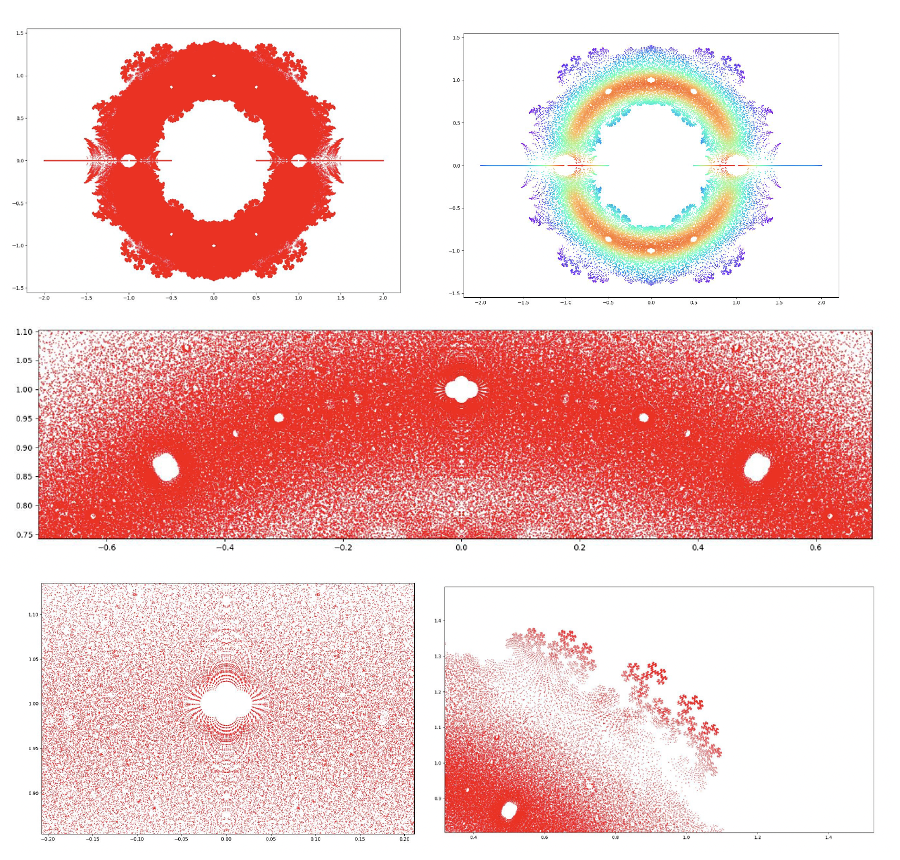
Visualising roots of algebraic numbers

Visualising the distribution of roots of integral polynomials of degree $n$ with coefficients either $1$ or $-1$ (e.g. here for degree at most $24$) leads to see fascinating patterns. For instance, one can do a systematic study of the distribution of the roots, investigate similarity between the inner part of the picture and these fractal dragons, connected question of the proportion of irreducible, "zoom" into some of the interesting parts of the picture of zeros, etc.

• 2023, Visualising roots of algebraic numbers II (EML, University of Luxembourg, in collaboration with Gabor Wiese)
• 2023, Visualising roots of algebraic numbers I (EML, University of Luxembourg, in collaboration with Gabor Wiese)

• Learn more

• Animation (degree 1-13)
• Animation (degree 12-17)

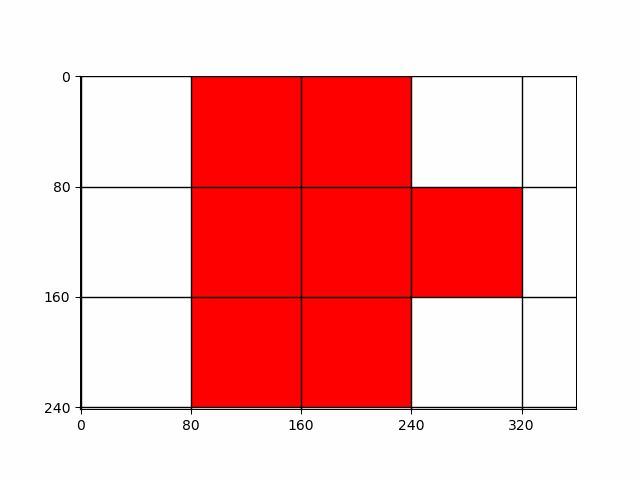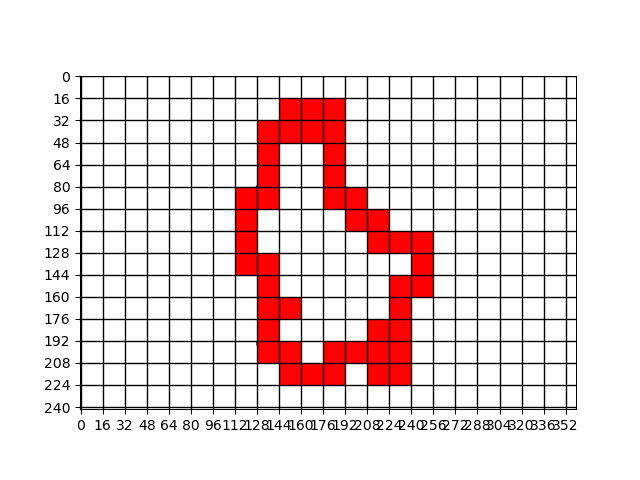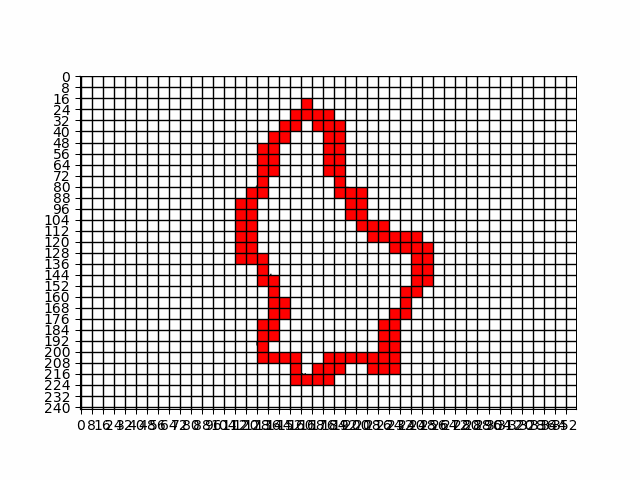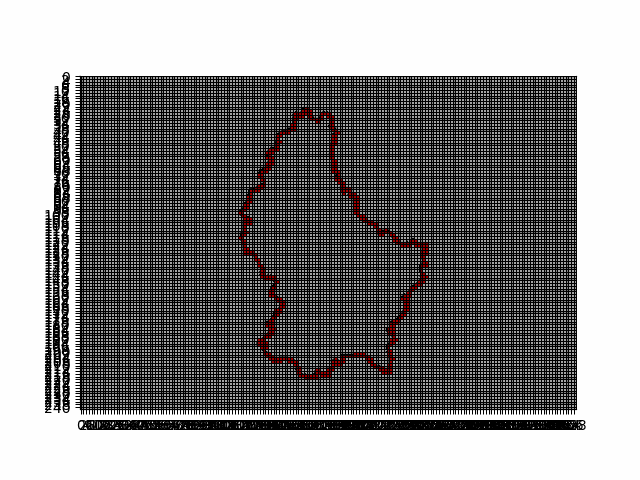
Lët'z box counting

The goal was to illustrate the map of our country, Luxembourg, using box-counting method.

• 2021, Lët'z box counting! (EML, University of Luxembourg, in collaboration with Lara Daw)

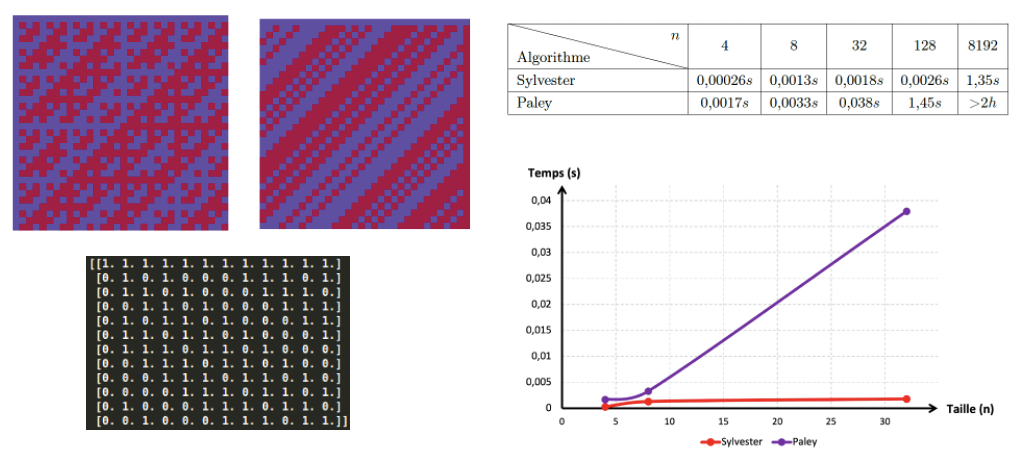
Playing with Hadmard matrices

Have you ever asked yourself how the pictures from spacecrafts are send back to Earth and how the scientists can recover the original image free of any errors? The answear lies in the error correcting codes, which are one technique for building in the appropriate redundancy. In 1990, NASA used a matrix of the augmented Hadamard code, called the Reed–Muller code, for the Mariner 9 mission. Speaking of Hadamard matrices, there is still an open question, known as the Hadamard conjecture. Until now, no one was able to prove that Hadamard matrix of order $4n$ exists for every positive integer $n$. For example, recently studies showed that Hadamard matrices of order $764$ exist!

• 2021, Behind the secrets of Hadamard matrices and their applications (EML, University of Luxembourg)

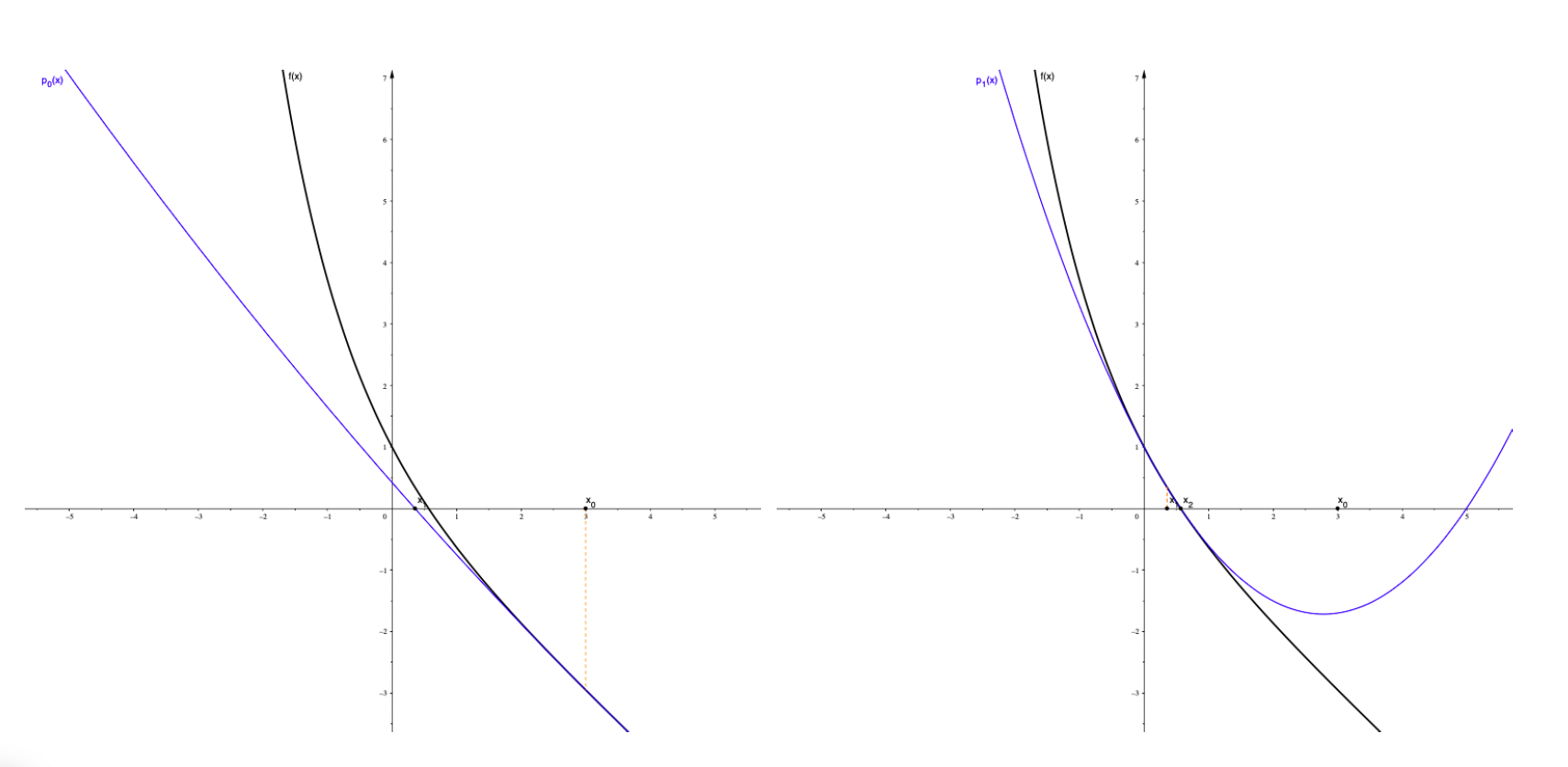
Solving polynomial equations over finite fields

The goal was to implement, to explore and to illustrate various methods for solving polynomial equations in one variable, e.g. over the real numbers using Newton approximation, over finite fields using Berlekamp's algorithm, etc.

• 2020, Solving polynomial equations (EML, University of Luxembourg, in collaboration with Gabor Wiese)

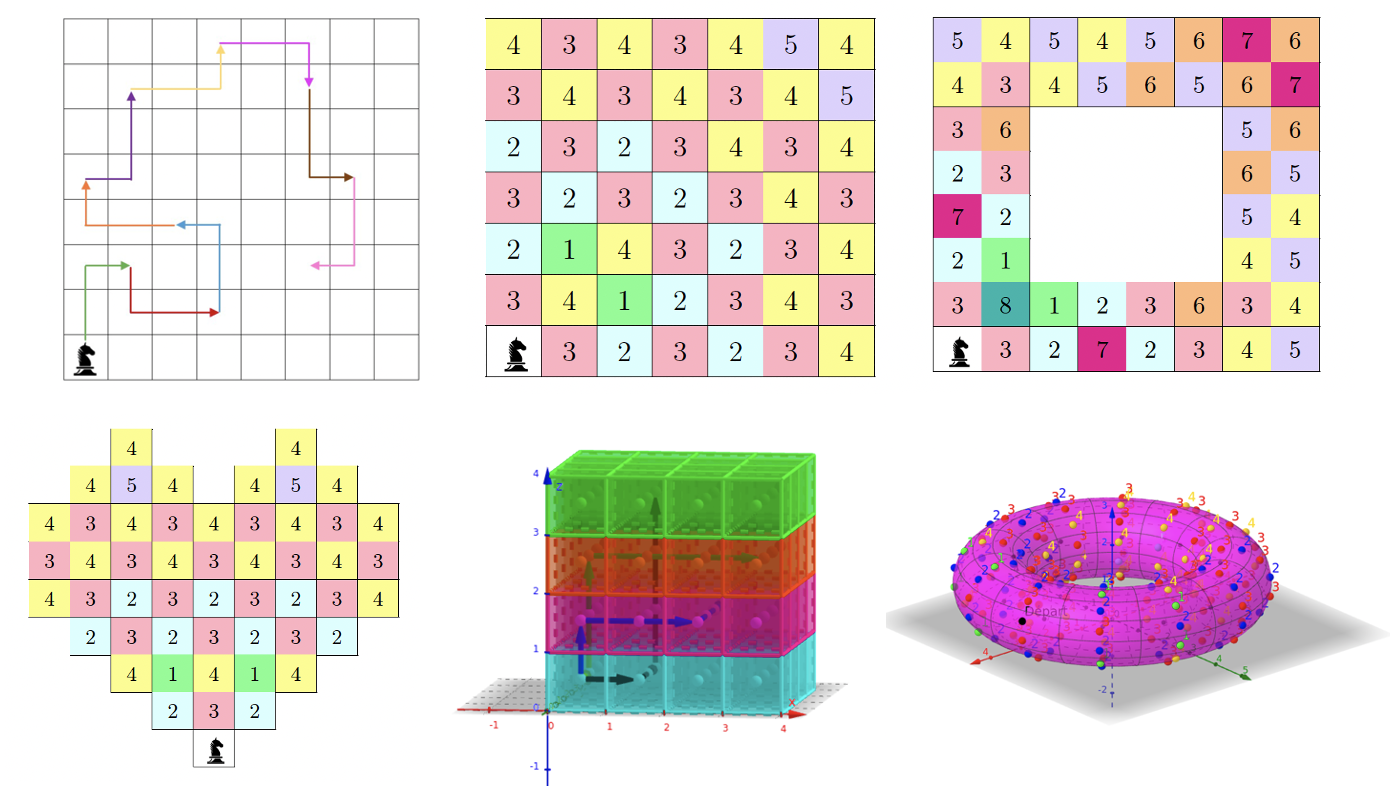
Playing with knights (and queens)

Among the famous chess inspired mathematical puzzles are those of the Knight's Tour and the Eight Queens. It is possible to make many variations of these puzzles on the usual board, but also on arbitrary chess boards, not necessarily square ones, of higher dimensions. The goal was to program these (and other) variations, illustrate them and make observations (for instance, on the (im)possibility for certain paths, the minimal length of paths, etc.).

• 2020, Knights (and queens)(EML, University of Luxembourg, in collaboration with Gabor Wiese)

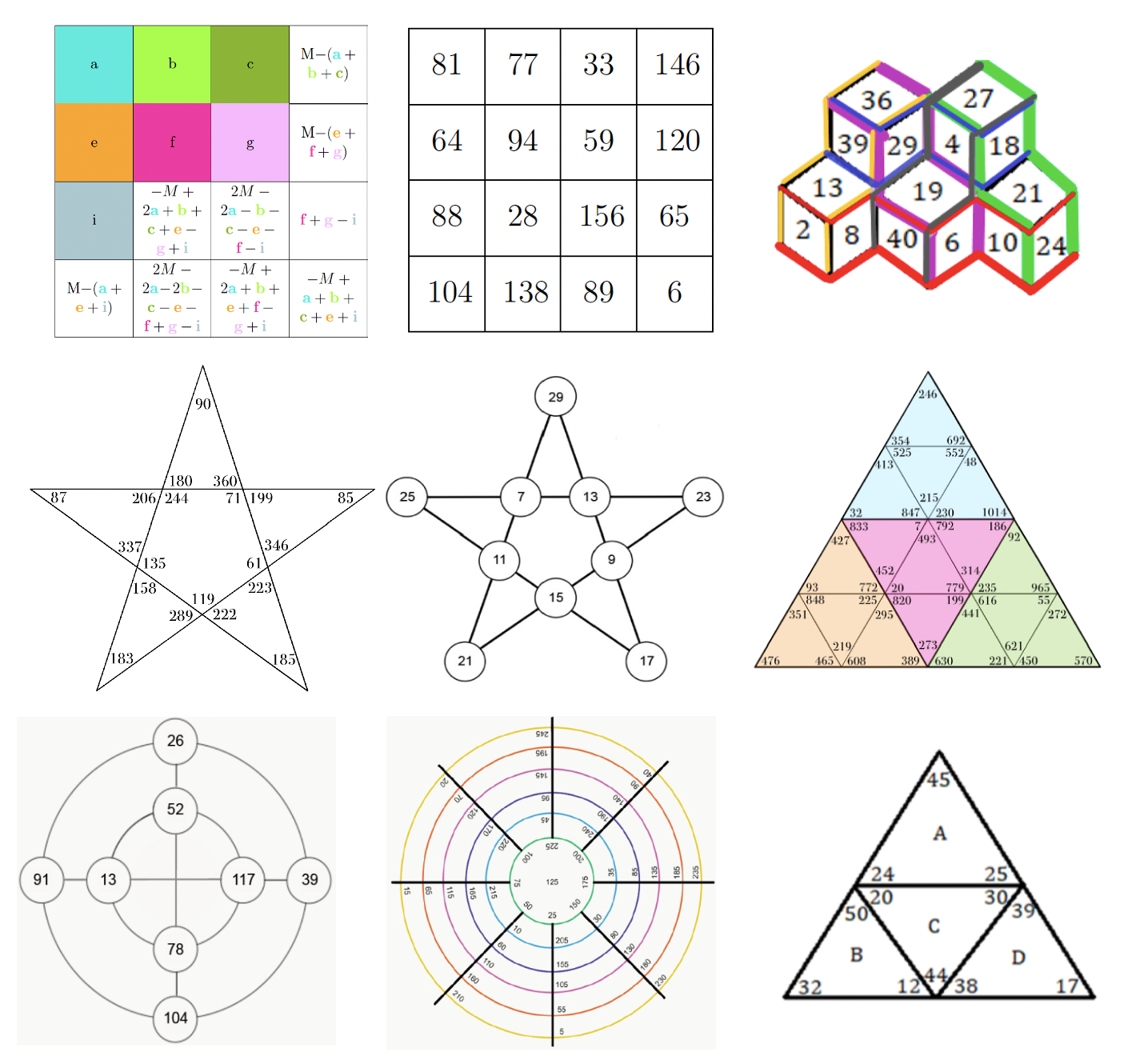
Magic objects of squares

A magic square is a square of distinct (usually positive) integers such that the sum of each row, each column and each diagonal is the same. A magic square of squares is a magic square such that each of its entries is a square. It is an open problem to decide if a $3 \times 3$ magic square of squares exists. Our students tested and created interesting variations: bimagic squares, magic cubes, "congruence magic squares of squares" using modular arithmetic, magic stars, magic stairs, etc.

• 2019, Magic squares of squares (EML, University of Luxembourg, in collaboration with Gabor Wiese)
• 2020, Magic objects of squares in modular arithmetic (EML, University of Luxembourg, in collaboration with Gabor Wiese)
• 2020, Magic objects over the integers (EML, University of Luxembourg, in collaboration with Gabor Wiese)
• 2024, "Magische Objekte in der Ebene" (Mathe am Computer, Universität Paderborn)
• 2024, "Magische Objekte aus Quadratzahlen: Modularer Ansatz" (Mathe am Computer, Universität Paderborn)
• 2024, "Magische Körper" (Mathe am Computer, Universität Paderborn)

• Learn more

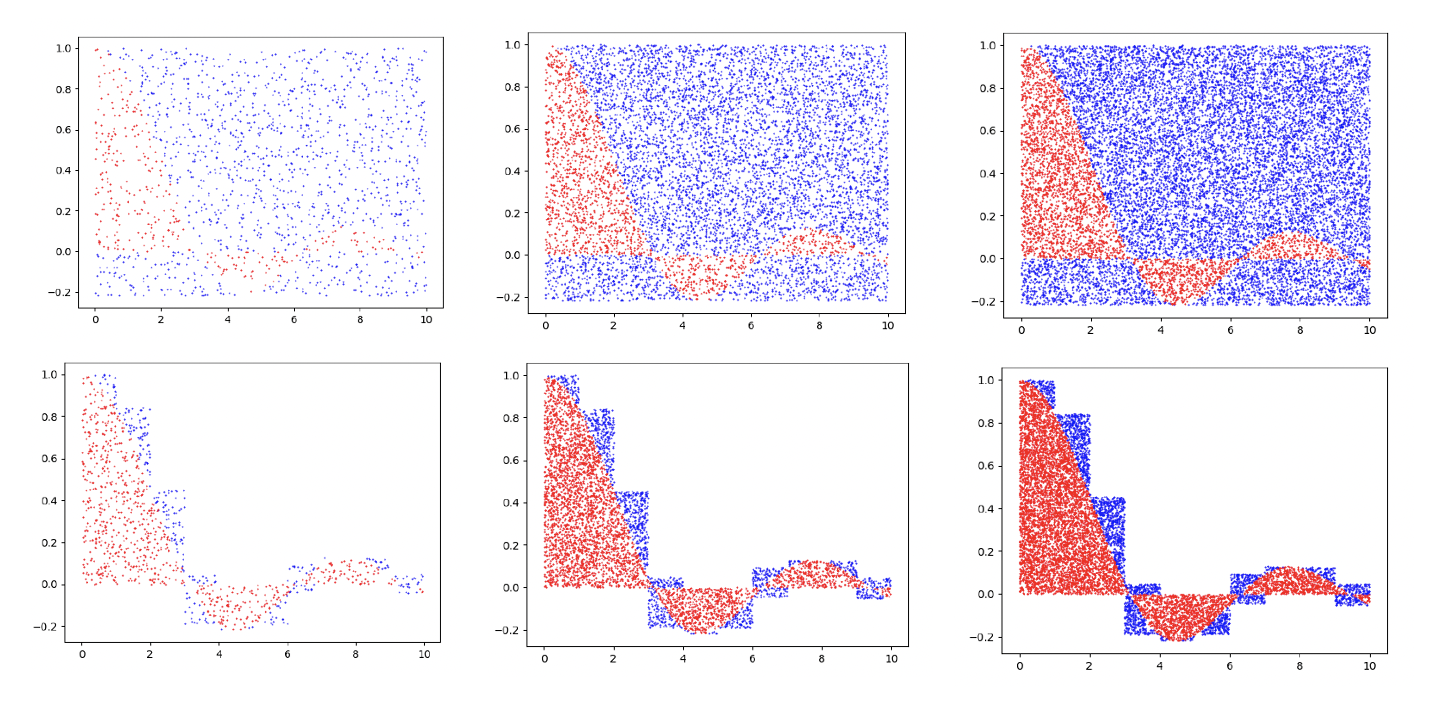
Approximating integrals thanks to Monte-Carlo

Monte Carlo methods are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. Their essential idea is using randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. The goal of this project was to vizualise and study several examples of situations where Monte Carlo estimation can be used.

• 2018, Monte Carlo simulation (EML, University of Luxembourg)

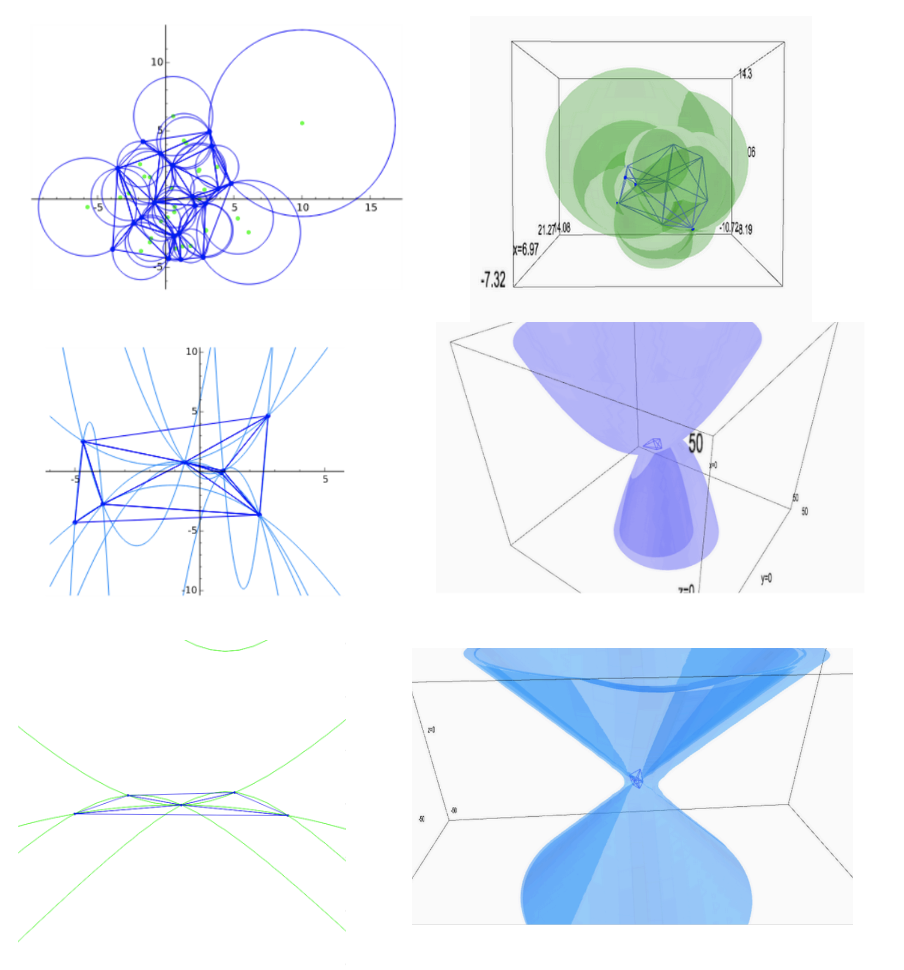
Exotic Delauny decomposition**

Given a set of points in the plane (resp. in Euclidean $3$-dimensional space, or in higher dimensions) one can define a "Delaunay triangulation" of their convex hull. More exotic types of Delaunay-like decompositions have been proved to exist, where the circles (resp. spheres) are replaced by special kinds of hyperboloids or paraboloids.

• 2018, Triangulation de Delaunay, student: Guenda Palmirotta (EML, University of Luxembourg)

** supervisor: Jean-Marc Schlenker